• Home
• Research
• Teaching
• Talks
• Activities
• Software & Data
• Blog

On stable equivalence of semialgebraic sets

About four months ago, I posted a question on MathOverflow concerning a lemma in Richter-Gebert’s book Realization spaces of polytopes. Let me quickly explain the setup. We are dealing with semialgebraic sets in $\mathbb{R}^d$ which are defined by polynomials with rational coefficients. A general semialgebraic set is defined by a Boolean combination of equations, inequations and (strict or weak) inequalities. If the only Boolean junction required to write the set is conjunction, then the set is basic and if, in addition, only equations and strict inequalities are required, it is primary basic.

Primary basic semialgebraic sets are (one possible choice of) building blocks for general semialgebraic sets and they are compactly specified by a polynomial system of the form $\{\, \phi_i(x) > 0, \, \psi_j(x) = 0 \,\}$ for $\phi_i, \psi_j \in \mathbb{Q}[x]$. On these sets one seeks a notion of equivalence which preserves multiple of their characteristics simultaneously, in particular the homotopy type and the algebraic number type, i.e., what is the smallest field extension over $\mathbb{Q}$ required to write down some point of the semialgebraic set? The definition of such a notion, called stable equivalence, in Richter-Gebert’s book is the subject of my question. Here it is:

Two primary basic semialgebraic sets $W$ and $V$ are rationally equivalent if there exists a homeomorphism between them which is in both directions defined by rational functions with rational coefficients. Next consider $W \subseteq \mathbb{R}^{n+m}$ and let $V \subseteq \mathbb{R}^n$ be its coordinate projection to the first $n$ coordinates. This is a stable projection if there exist polynomials $\phi_i, \psi_j \in \mathbb{Q}[v,w]$ which have degree 1 in the coordinates $w$ and such that we may recover $W$ from its projection $V$ via

$W = \{\, (v,w) \in \mathbb{R}^{n+m} : v \in V, \; \phi_i(v,w) > 0, \; \psi_j(v,w) = 0 \,\}.$

The sets are stably equivalent if they are in the same class of the smallest equivalence relation which is generated by rational equivalence and stable projection. Richter-Gebert states in his Lemma 2.5.2 that stably equivalent sets have the same homotopy type and algebraic number type. This is pretty obvious for the rational equivalences. In the rest of this article, I will concentrate on the stable projection part of this claim.

You may be wondering why the polynomials need to be affine-linear in the coordinates $w$ which should be “recovered” from the projection $V$. This is required to preserve the algebraic number type. Solving equations of higher degree, such as $w^2 = 2$ may increase this measure of algebraic complexity, while linear equations surely do not. The proof for the algebraic number type in the book is slightly wrong but easily fixable and the statement holds (if the equations are affine, then there need not be purely rational $w$ coordinates, as is claimed, for every $v \in V$ but Cramer’s rule implies that their coordinates are in the field extension of $\mathbb{Q}$ generated by $v$). This is the reason for restricting to affine-linear equations. To prevent a lingering confusion at this point, let me clarify that the inequalities being affine-linear is not necessary for any argument presented here — they could be non-linear if needed.

Notice that in the above definition, every fiber $F_v = \pi^{-1}(v)$ is the relative interior of a polyhedron. For my dissertation, I needed to extend this machinery to fibers which are more general convex sets, namely spectrahedra (the intersections of affine-linear spaces of symmetric matrices with the cone of positive-semidefinite matrices) — in that case I need some non-linear inequalities. The problem: there is no proof given in the book for the homotopy equivalence claim from which I could start. This led to my MathOverflow question.

A counterexample

My initial hope was to find a general theorem in a topology textbook of the sort “this diagram chase constructs a section, therefore the two spaces are homotopy-equivalent” but that did not happen. In the sections of Hatcher’s Algebraic Topology dedicated to fiber bundles and fibrations I found theorems that say, when $V$ is contractible, then we essentially have a fiber bundle. But the idea behind a stable projection is different: we want to deduce from the fact that the fibers $F_v$ are uniformly defined (by the polynomials $\phi_i$ and $\psi_j$) and extremely simple (they are polyhedra, therefore convex and homotopically trivial with something as simple as straight line homotopies), that $V$ and $W$ should not differ in terms of homotopy. I discussed this view at length with my colleagues Andreas Kretschmer and Yuri Santos Rego for whose time and input I’m very thankful. This eventually led to the following simple counterexample to the claim in the book:

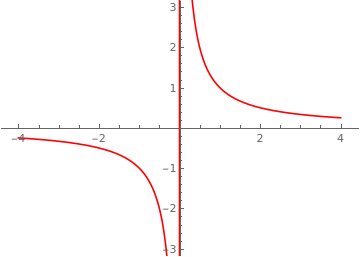
Consider $W = \{\, (v,w) \in \mathbb{R}^2 : v(vw - 1) = 0 \,\}$. This set is the union of the $w$-axis with the hyperbola $vw = 1$. Its projection onto the $v$-coordinate is the entire real line $V = \mathbb{R}^1$ and the definition of $W$ already proves that this projection is stable, because there is one equation defining $W$ in terms of $v \in \mathbb{R}$ which has degree 1 in $w$. But the line $V$ is path-connected whereas $W$ is not: for $v \to 0^+$, the unique coordinate $w$ with $(v,w) \in W$ tends to $+\infty$ while with $v \to 0^-$, this $w$ tends to $-\infty$. At $v=0$, all $w$ give a point in the fiber $F_0$, but this does not path-connect the two branches of the hyperbola in the affine plane. Two spaces which differ in their path-connectedness cannot be homotopy-equivalent.

This counterexample can be “homogenized” to

$W = \{\, (v, w, w') \in \mathbb{R}^3 : w' > 0, \; v(vw - w') = 0 \,\}$

so that its fibers are defined by homogeneous linear forms in $w$. The space $W$ and its projection $V$ still differ in path-connectedness and therefore are a counterexample to homotopy equivalence under the slightly more restricted definition of stable projection in the article by Richter-Gebert and Ziegler: Realization spaces of 4-polytopes are universal.

Local sections are sufficient (but not necessary)

In the months following that discovery I think I obtained a fairly good understanding of why the definition in Richter-Gebert’s book fails to give homotopy equivalence and what can be done to fix it. This is in no small part thanks to resources pointed out by Richter-Gebert about earlier attempts to give a satisfying notion of stable equivalence, including his own variants of the definition. These are described in the last section. Before that, I want to give a few technical remarks and proof snippets from my perspective as a topology pedestrian.

Let us assume that $W$ and $V$ are primary basic semialgebraic sets, $V$ is the projection of $W$ and it is stable in the sense that $W = \{\, (v,w) \in \mathbb{R}^{n+m} : v \in V, \; \phi_i(v,w) > 0, \; \psi_j(v,w) = 0 \,\}$, where I’m leaving the precise restrictions on $\phi_i$ and $\psi_j$ unstated for the moment. But let’s assume that they are polynomials and that each fiber $F_v$ is a convex set.

The most natural approach to proving homotopy equivalence of the set $W$ to its stable projection $V$ is to obtain a covering of it by local sections for the projection $\pi$. That is, for every $v \in V$ a small neighborhood $U_v$ around $v$ and a continuous map $s_v: V \cap U_v \to W$ such that $\pi \circ s_v$ is the identity.

To show that this is sufficient for homotopy equivalence, let me recite some basic facts about the topology on semialgebraic sets. These facts can be pieced together from general results found among the first 40 pages of Bredon’s book Topology and geometry. Consider a primary basic semialgebraic set with its induced euclidean topology. This is surely a second-countable Hausdorff space because its ambient $\mathbb{R}^n$ is. It is locally closed (immediate from its defining polynomials) and locally compact which implies that it is paracompact. This in turn ensures the existence of subordinate partitions of unity to any open covering.

In a paracompact space, we may assume that $(U_v)_{v \in V}$ has been thinned out to a locally finite cover $(U_v)_{v \in V'}$ indexed by a subset $V' \subseteq V$. Then, we obtain functions $\rho_v$ which partition unity on $V$ and such that the support of $\rho_v$ is confined to a closed set inside $U_v$. This allows us to define a global section $s(\tilde v) := \sum_{v \in V'} \rho_v(\tilde v) s_v(\tilde v).$ That this summation is finite follows from the local finiteness of the partition of unity. It is well-defined because $\rho_v(\tilde v)$ vanishes outside of the domain of $s_v$ due to the subordination of the $\rho$’s. The function is continuous because $\rho_v$ and $s_v$ are continuous. Lastly, the sum is a convex combination of $s_v(\tilde v)$ over finitely many $v \in V$. By definition $s_v$ satisfies $s_v(\tilde v) \in F_{\tilde v}$ and $\pi(s_v(\tilde v)) = \tilde v$. Since the fiber $F_{\tilde v}$ is convex, this convex combination remains inside it. Thus $s$ is a section of $\pi$.

As an aside: By standard analysis constructions, we can even demand $\rho_v$ smooth on the open neighborhood $\bigcup_v U_v$ of $V$. Hence, the differentiability properties of $s$ depend entirely on how smooth we are able to make the local sections $s_v$, but in the following I want to focus on the existence of continuous local sections only. You are invited to keep this in mind for the time when local sections are constructed.

Having the global section $s: V \to W$ of $\pi$, it is easy to recognize that $s(V)$, which is a homeomorphic copy of $V$ inside of $W$, is in fact a strong deformation retract of $W$: since the fibers over $V$ are convex sets, straight-line homotopies retract $W$ onto $s(V) \subseteq W$. All we needed the section $s$ for was to choose a “representative point” continuously for every fiber of $V$ on $W$. The homotopy itself is then very easy. This yields homotopy equivalence from local sections.

However, not every homotopy equivalence allows for the existence of local sections. Consider the semialgebraic set $W = \{\, v < 0, \, w = -1 \,\} \cup \{\, v = 0, \, -1 \le w \le 1 \,\} \cup \{\, v > 0, \, w = 1 \,\}$:

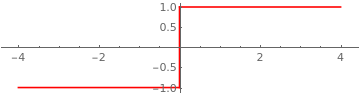
This space is homeomorphic to a line $\mathbb{R}^1 \subseteq \mathbb{R}^2$. Its projection onto the $v$-axis is the line $\mathbb{R}^1$ as well. Thus, we have homotopy equivalence but a local section at $v=0$ does not exist because $W$ is almost everywhere the graph of a discontinuous function around $v=0$.

The difficulty of obtaining local sections

Let’s see what the problem is with obtaining local sections in our setting. Fix $v \in V$ and we may fix a point $(v,w) \in F_v$. The goal is to extend this particular solution $w$ to the system $\phi_i(v,w) > 0$ and $\psi_j(v,w) = 0$ continuously to a small neighborhood of $v$. Locally, the strict inequalities $\phi_i > 0$ make no problems at all, so we concentrate on the equations $\psi_j = 0$. Now it simplifies the situation to assume that they are linear in $w$ and write them as a system $A_v w = b_v$ where $A_v$ is a matrix whose entries are polynomials in $v$ and $b_v$ is a column vector of that sort. This system may be square, under- or overdetermined.

The parametrized family of matrices $A_v$ has a generic rank in the affine space $\mathbb{R}^n$. Let $v$ be any point in $\mathbb{R}^n$ and consider a minimal spanning set of columns of $A_v$. Their number $r$ is the rank and for them to be linearly independent means that there is a square submatrix in this collection of columns whose determinant does not vanish. Consider this same subdeterminant of $A_v$ as a polynomial in $v$. Since it does not vanish for some $v \in \mathbb{R}^n$, its zero locus is a lower-dimensional variety and thus the rank of $A_v$ is at least $r$ outside of this locus. This shows that the maximum rank of any particular $A_v$, $v \in \mathbb{R}^n$, is in fact the rank attained by $A_v$ almost everywhere. In every sufficiently small neighborhood of $v$, the rank of $A_v$ can only increase (if it does increase, that means $v$ is one of those special points in the vanishing locus of a determinant) — equivalently, the dimension of the solution space to the homogeneous equations $A_v w = 0$ can only decrease. This holds on every irreducible real algebraic variety $V$ in place of $\mathbb{R}^n$ (the generic rank might be lower than on the entire space but that lower rank will be attained almost everywhere), but it is not necessarily true on primary semialgebraic sets.

Brushing that issue aside, if the rank is locally constant, that is, the generic rank is attained on every single point inside an open neighborhood of any chosen $v$, then local sections are easy to construct by applying Cramer’s rule to the full-rank square submatrix examined in the previous paragraph: the particular solution $w$ extends to a unique surface of solutions for the systems $A_v w = b_v$ around $v$. A problem arises only at those points where the generic rank rises in every neighborhood. This is precisely the failure mode of the above counterexample at $v=0$.

Stable equivalence kaleidoscope

After these detailed preparations, we are ready to see notions of stable projection which preserve homotopy type.

Constant-dimension Richter-Gebert

As argued in the previous section, if Richter-Gebert’s definition of stable projection would be strengthened to require that the fiber polyhedra have the same dimension locally around every point of $V$, then we obtain local and, by convexity and partitions of unity, a global section.

Separated equations and inequalities

Suppose that the fibers in a stable projection are convex and are described either by (non-linear) strict inequalities or by linear equations in $w$. In the case of strict inequalities, local sections obviously exist because around a given point $(v,w) \in F_v$ any $v'$ close enough to $v$ can just use $(v',w) \in F_{v'}$ by continuity of the strict inequalities. In the case of only linear equations, we have the global section $v \mapsto (v,0)$. If you can decompose your projection into a sequence of such simple projections, homotopy equivalence follows.

The hyperbola counterexample above uses only a single affine equation in $w$, so even if inequalities and equations are separated in the definition, affine equations are not admissible.

Bokowski and Sturmfels: product with $\mathbb{R}^m$

In their fantastic book Computational synthetic geometry, Section 6.3, Bokowski and Sturmfels give a concise definition of stable equivalence while discussing the universality theorem of Mnëv which was brand new at the time. Two semialgebraic sets $V$ and $W$ are stably equivalent according to Bokowski and Sturmfels if there exists a locally biregular homeomorphism $f$ such that $f(V \times \mathbb{R}^m) = W$. In this setup, rational equivalence and stable projection have been fused into one concept represented by the map $f$. The homotopy equivalence of $V$ and $W$ is obvious: $V$ is just $V \times \{\,0\,\}$ which is a deformation retract of $V \times \mathbb{R}^m$ and this is in turn homeomorphic to $W$.

Günzel: product with a manifold

Günzel in The universal partition theorem for oriented matroids has a very similar definition of equivalence. He is interested in differential-geometric features, so the restriction to polynomials is dropped. The space $\mathbb{R}^m$ is replaced by a smooth manifold $N$ under a diffeomorphism $f$. As far as I can see, the manifold is not claimed to be contractible, so that this does not necessarily entail homotopy equivalence of $V$ and $W = f(V \times N)$. But if $N$ is contractible, then the proof is as easy as above. In any case, this product with a smooth manifold is probably the preservance of the “singularity structure” mentioned in Richter-Gebert and Ziegler’s bulletin cited above. This claim does not appear in the book version of the lemma.

Affine assignments and non-linear inequalities

In my own work about a universality theorem for Gaussian conditional independence models, I wanted to recover homotopy and algebraic number type as well as algorithmic complexity which is why I favor maps defined globally by polynomials instead of locally, as in Bokowski-Sturmfels. In addition, I found Richter-Gebert’s view of uniformly varying fibers more convenient in proofs than having this map around a product with $\mathbb{R}^m$.

What I really needed for my spectrahedral fibers were affine-linear equalities in $w$ which were shown above to cause problems if the dimension of the solution space can vary. In my case, this could be cured by always having zero-dimensional linear spaces in the definition of the fibers. In fact, the definition of stable projection I use in my thesis is this: $W$ must be recoverable from $V$ as all $(v,w',w'')$ satisfying $v \in V$, $\phi_i(v,w') > 0$ and $w_j'' = \psi_j(v)$, where $\phi_i$ and $\psi_j$ are arbitrary rational functions such that all fibers are convex. The only equations are direct assignments of rational functions in $v$ to a subset $w''$ of the lost coordinates. This may seem like a serious limitation but the Shor normal form, which plays an important role in the universality theorem for 4-polytopes as well, still works with affine assignments and convex fibers only. The existence of local sections is immediate and since the fibers are convex, the previous arguments for the existence of a global section apply.

Conclusion

My verdict on this issue is that the fibers need to have constant dimension. Convexity, unexpectedly, plays a large role in the proofs I presented, as they rely on a partition of unity to paste local sections together.

This was a long article which resulted from reading some amazing papers from the 90s and many long discussions with my colleagues in Magdeburg. I think I’ve gained a solid understanding of the problem and possible fixes. The exposition of this topic had a month or two more delay than they should have had because my thesis submission, the move to Leipzig and new projects took precedence. And it is still not over. I am in contact with Jürgen Richter-Gebert about the problem in his book and we are looking to establish a reading group with the aim of publishing a correction note in due time.

Addendum (27 Mar 2024): The task of finding suitable definitions for stable equivalence and checking the validity of Richter-Gebert’s proofs under these new definitions has been successfully tackled by Emil Verkama in this M.Sc. thesis Repairing the Universality Theorem for 4-Polytopes for which he won the Ernst Lindelöf prize of the Finnish Mathematical Society.