A rational realization of Šimeček’s № 85

In his article Gaussian Representation of Independence Models over Four Random Variables from 2006, Petr Šimeček lists all conditional independence structures (or “independence models”) which are realizable by Gaussian distributions, regular or not, in dimension 4. For each model he gives a concrete correlation matrix which realizes it. Only one of these examples, named M85, is displayed with irrational entries. Šimeček asks in his article whether all Gaussian CI structures can be realized with rational correlations.

When I was at the Prague Stochastics Workshop in memory of František Matúš last year, the same question came up and the remark quickly passed the room that Šimeček had left this model M85 unresolved — a concrete example to work on. This is how I learned about his interesting paper and the excesses of singular Gaussians. Today I allowed myself to get side-tracked and see if M85 was really inherently irrational.

The short answer is: no, it also has a rational correlation matrix. Consequently, as far as I’m aware, the conjecture about rationality of Gaussian CI remains open.

Gaussian conditional independence

We consider a random vector $\xi$ with entries $\xi_1, \dots, \xi_n$ which is distributed according to a Gaussian distribution with a positive-semidefinite covariance matrix $\Sigma$ . Of interest of this vector is its conditional independence (CI) structure, which is the collection of all statements $\xi_i \CI \xi_j \; | \; \xi_K \quad \text{abbreviated as $(ij|K)$}$ for $i, j \in [n]$ different and $K \subseteq [n] \setminus \{i,j\}$ , which hold for the distribution. This statement means that learning the value of the coordinate $\xi_i$ does not tell us anything about $\xi_j$ if we already know all the coordinates $\xi_k$ for $k \in K$ .

What structure does this set of all CI statements have? For Gaussian distributions a particularly intriguing characterization is known. To decide whether $(ij|K)$ holds, determine an inclusion-maximal set $L \subseteq K$ such that the principal minor $\det \Sigma_{L}$ does not vanish. Then $(ij|K)$ holds if and only if the almost-principal minor $\det \Sigma_{iL,jL}$ does vanish. In particular if the Gaussian is regular (equivalently, if $\Sigma$ is positive-definite) then we always choose $L = K$ in this test.

If we are given some CI structure $\mathcal{A}$ as a collection of symbols $(ij|K)$ , then in order to decide if it has a regular Gaussian realization, we have to concatenate polynomial equations, inequations and inequalities in the $\binom{n+1}{2}$ unknowns which are the entries of the symmetric matrix $\Sigma$ :

The first couple of inequalities $\det \Sigma_I > 0$ , $I \subseteq [n]$ state that the matrix be positive-definite,
we add equations $\det \Sigma_{iK,jK} = 0$ for $(ij|K) \in \mathcal{A}$ for the CI statements we wish to hold,
and then inequations $\det \Sigma_{iK,jK} \ne 0$ for $(ij|K) \notin \mathcal{A}$ to exclude all other CI statements.

Notice that deciding whether the space of these matrices $\Sigma$ is empty or not is a semialgebraic decision problem. All polynomials are determinants of a symmetric matrix, which makes Gaussian CI particularly exciting.

The above only describes regular Gaussian realizations. For singular realizations we would have to pick in the first step which principal minors should vanish. These choices would affect which almost-principal minors to evaluate in steps 2 and 3 to model CI statements. Clearly, it gets a little more complicated overall as more choice is added. Of course, there are CI structures which are realizable by singular and not regular Gaussians, such as our № 85.

As a final remark to this section, there is a well-known lemma that allows us to pass to a special kind of covariance matrix which has all $1$ s on the diagonal (so is simultaneously the distribution’s correlation matrix) without changing the CI structure of the random vector. This trick reduces the number of variables in our semialgebraic system from $\binom{n+1}{2}$ to $\binom{n}{2}$ as it eliminates the $n$ variances on the diagonal.

The model № 85 and (part of) its realization space

Below is the CI structure M85 with its irrational realization, copied straight from Šimeček’s paper.

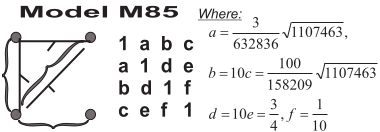
Šimeček’s model № 85 as presented in the paper.

The style of diagram on the left was developed by Radim Lněnička to encode CI structures on four random variables. It reads

$\mathsf{M85} := \{ (12|4), (14|3), (14|23), (24|3), (24|13), (34|12) \}.$

In the previous section, I have outlined an algorithm to describe all the positive-semidefinite matrices which realize a given CI structure, such as $\mathsf{M85}$ . Since we want a non-regular realization (there is no regular realization because $\mathsf{M85}$ is not a gaussoid), we have to make some decisions about which principal submatrices we want to be zero and which positive.

For the CI statements in $\mathsf{M85}$ , we care about the principal minors of the sets $4$ , $3$ , $23$ , $13$ and $12$ . The minors of singleton sets are already equal to $1$ when we work with correlation matrices. The only non-trivial assumptions we make are that $\Sigma_{12}$ , $\Sigma_{13}$ and $\Sigma_{23}$ are positive. Then we can write down equations for the CI statements in $\mathsf{M85}$ as if the matrix $\Sigma$ was regular. Suppose

$\Sigma = \begin{pmatrix} 1 & a & b & c \\ a & 1 & d & e \\ b & d & 1 & f \\ c & e & f & 1 \end{pmatrix},$

then we obtain the following equalities:

$(12|4)$ : $a = ce$ ,
$(14|3)$ : $c = bf$ ,
$(24|3)$ : $e = df$ ,
$(14|23)$ : $c + adf + bde = ae + bf + cd^2$ ,
$(24|13)$ : $e + abf + bcd = ac + b^2e + df$ ,
$(34|12)$ : $f + abe + acd = a^2f + bc + de$ .

Using the first three equalities and the requirement that all variables be non-zero, we see that $(14|23)$ and $(24|13)$ both reduce to the equality $cd = be$ which already follows from the simpler equalities: $cd = (bf)d = b(df) = be$ .

Moreover notice that $a$ is determined by $c$ and $e$ , $c$ by $b$ and $f$ and $e$ by $d$ and $f$ , and even in a way that preserves rationality. If we can find rational $b,d,f$ which satisfy the equality of $(34|12)$ , then we have all rational entries which satisfy all the equations required.

Eliminating all $a, c, e$ from equation $(34|12)$ , we obtain equivalently

$1 = f^4 b^2 d^2 + b^2 + d^2 - 2 b^2 d^2 f^2.$

I substituted $b = p/q$ , $d = s/t$ , $f = x/y$ and asked Mathematica for integer solutions in $p,q,s,t,x,y$ to the above equality together with some of the inequality constraints like $0 < (p/q)^2 < 1$ etc. and it reported back a solution after maybe 10 seconds, which lifts to:

$b = -\frac{49}{51}$ , $d = \frac{1}{3}$ , $f = \frac{63}{147}$ ,
$c = -\frac{7}{17}$ , $e = \frac{1}{7}$ ,
$a = -\frac{1}{17}$ .

My Julia code indeed confirms that this matrix is a positive-semidefinite realization of $\mathsf{M85}$ . The singular principal minors are $123$ and $1234$ . My apologies to whoever expected clever arguments at this point. Mathematica simply beat me to it. It was very fortunate that all the inequalities and inequations seemed to fall into place once the equalities were satisfied rationally.

Rationality conjectures

The conjecture that all Gaussian CI structures are realizable by rational correlation matrices is still unresolved, even in the special case of regular Gaussians. By the way, there is an analogous conjecture by Matúš about discrete (as opposed to Gaussian) CI structures with an adapted notion of rationality on the last page of his paper Conditional independences among four random variables III: final conclusion. And finally, rationality in a somewhat different flavor is mentioned in Question 2 in Studený’s book, p. 190: is the conical closure of discrete multiinformation functions a rational polyhedron?

Likewise I am not aware of a solution to these conjectures. If you know of updates, please do let me know.

Addendum (26 May 2020): The conical closure of discrete multiinformations is a linear image of the entropy region and while I have not proved it in detail, I would suspect that Matúš’s breakthrough carries over to show that discrete multiinformations do not form a rational polyhedron, because they are not even a polyhedron.

Addendum (3 Mar 2021): I answer Šimeček’s question negatively in my recent preprint “Incidence geometry in the projective plane via almost-principal minors of symmetric matrices”.